در این مبحث به عنوان روش اصلی برای تحلیل ساختمان در مقابـل فشـارهای ناشـی از انفجـار، از روش دینامیکی غیرارتجاعی و برای طراحی از معیارهای تغییرشکل شامل ضریب شکل پـذیری (μ) و دورانهـای انتهـایی اعضـا و مفـاهیم عملکـردی اسـتفاده مـیشـود. بـه عنـوان روش جـایگزین، روش تجویزی استاتیکی معادل نیز مورد استفاده قرار می گیـرد. حـوزه شـمول ایـن فصـل مطـابق جدول ٢١-١-٢-الف میباشد.
٢١-٥-١- تحلیل دینامیکی غیرارتجاعی سازه یک درجه آزادی (SDOF)
مدل تحلیلی پایه، که بیشترین کاربرد را در طراحی انفجـاری دارد، روش سـازه یـک درجـه آزادی معادل ارتجاعی- خمیری کامل[1] (الاستوپلاستیک کامل) میباشد.
٢١-٥-١-١- سازه یک درجه آزادی معادل
اغلب اعضای سازه ها، دارای بیش از یکدرجه آزادی هستند، اما بسیاری از آنها را می توان با دقـت کافی به سازه های یکدرجه آزادی معادل، تبدیل نمود.
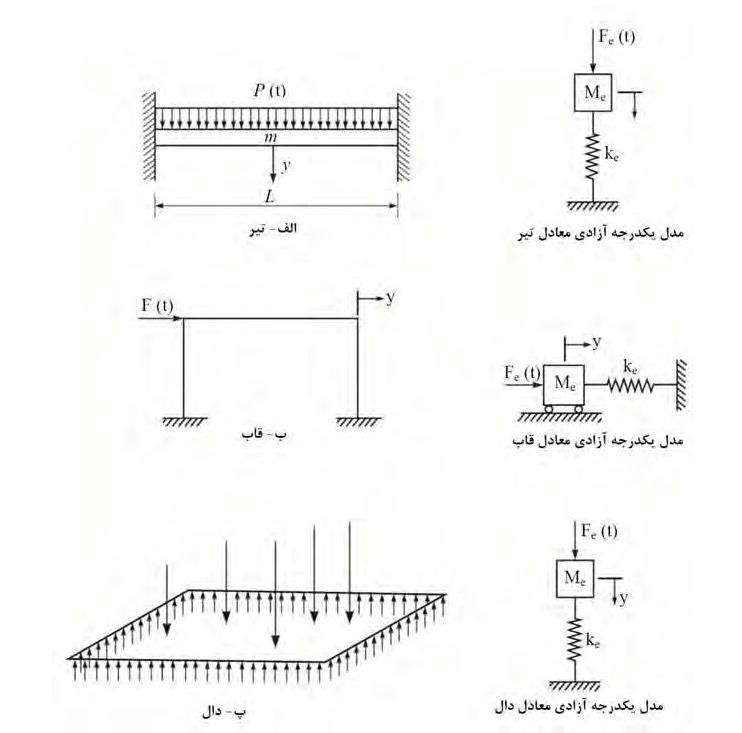
بسیاری از تحلیل های دینامیکی سازه های مقاوم در برابر انفجار، بر مبنـای سـازه یـکدرجـه آزادی معادل است. عناصر اصلی در معرض فشار مستقیم انفجـار نظیـر قـابهـای صـفحهای یـک طبقـه، دیوارهای طره ای، تیرها و دال ها، قابل معادل سـازی بـا سـازة یـکدرجـه آزادی مـی باشـند (شـکل ٢١-٥-١). در مدل یکدرجه آزادی معادل، مفاهیم نیروی خارجی، جرم و سختی با نیروی معـادل (Fe)، جرم معادل (Me) و سختی معادل (Ke) جایگزین می شوند که در بنـد ٢١-٥-١-٤ تعریـف میشوند.
٢١-٥-١-٢- بار دینامیکی ایضربه
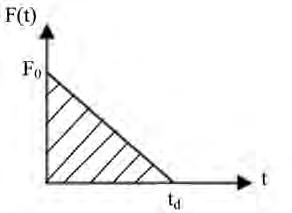
بار تابع زمان انفجار را می توان مطابق شکل ٢١-٥-٢ بصورت مثلثی مدل کرد که مقدار حداکثر آن Fo و مدت تأثیر آن بر سازه td میباشد. در نتیجه نیروی تابع زمان برابر خواهد شد با:
| (1-5-21) |
ضربه انفجار (i) تقریباً، مساوی سطح زیر نمودار بارگذاری است و از رابطه زیر به دست میآید:
| (2-5-21) |
٢١-٥-١-٣- سازه یک درجه آزادی ارتجاعی- خمیری
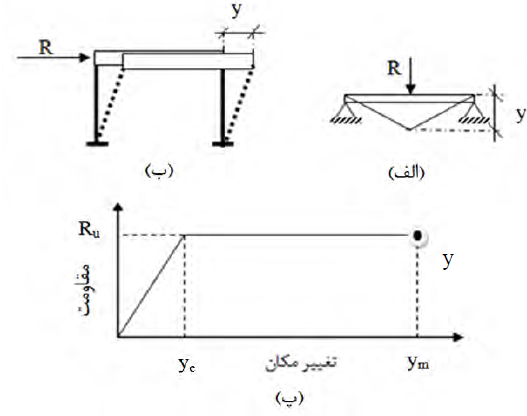
در شـکلهـای ٢١-٥-٣-الـف و ب سـازه هـای یـکدرجـه آزادی ارتجـاعی- خمیـری و در شـکل ٢١-٥-٣-پ نمودار مقاومت سازه در مقابل تغییرشکل آن رسم شده است.
در این شکل R نیروی وارده، Ru مقاومت نهایی سازه یکدرجه آزادی است.
با توجه به شکل ٢١-٥-٣-پ، ضریب شکل پذیری سازه ارتجاعی- خمیـری (μ)، از رابطـه زیـر بـه دست میآید:
| (3-5-21) |
٢١-٥-١-٤- ضرائب تبدیل به سازه یک درجه آزادی معادل خمیری- ارتجاعی
برای تبدیل سازه با جرم، سختی و بارگذاری گسترده به سازه یـکدرجـه آزادی معـادل ارتجـاعی- خمیری، از ضرائب تبدیل استفاده میشود. مقادیر جـرم معـادل، سـختی معـادل، نیـروی معـادل و مقاومت معادل با استفاده از ضرائب تبدیل، از روابط زیر به دست میآیند:
| (4-5-21) |
سختی معادل Ke = K L × K جرم معادل Me = K M ×M نیروی معادل Fe = K L ×F مقاومت معادل Re = K L × R |
| (5-5-21) |
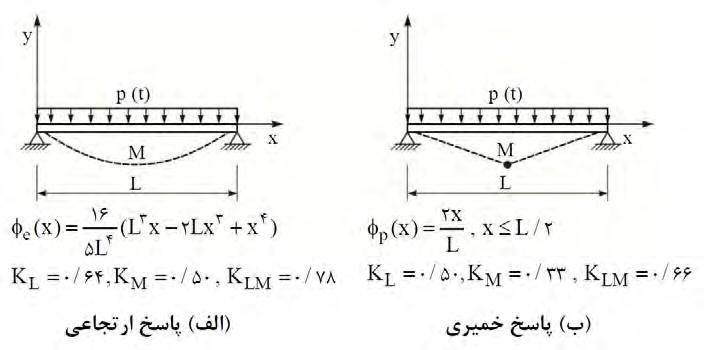
مقادیر ضرایب تبدیل، بستگی به نوع تغییرشکل عضو سازه ای دارند. به عنوان مثال، برای تیر سـاده شکل ٢١-٥-٤، بر حسب نـوع تغییرشـکل در رفتـار ارتجـاعی و خمیـری، مقـادیر ضـرایب تبـدیل متفاوتی بدست می آید. در موارد عملی ضرائب تبدیل در طول تحلیل، ثابت فرض مـی شـوند. بـرای انتخاب ضرایب مناسب، از قضاوت مهندسی و متناسب با ماهیت پاسخ حاکم سازه (عضو)، اسـتفاده می شود. گاهی از میانگین ضرایب انتقال ارتجاعی و خمیری نیز استفاده می شـود. درصـورت تغییـر رفتار اعضای سازه از حالت ارتجاعی به خمیری و بر عکس ضرایب تبدیل نیز تغییر میکنند.
ضرایب تبدیل و روابط واکنش های تکیه گاهی اعضـای مختلـف بـرای بارگـذاری و شـرایط مختلـف تکیه گاهی، در جداول ٢١-٥-١ تا ٣ ارائه شده است. در این جدول ها، Mpc ظرفیت خمشی نهـایی اسمی مقطع در وسط دهانه و Mps ظرفیت خمشی نهایی اسمی مقطع در تکیـه گـاه اسـت کـه بـا ضرب مقاومت مصالح در ضرایب افزایش مقاومت و افـزایش دینـامیکی (DIF و SIF ) و بـا فـرض ضرایبهای تقلیل ظرفیت برابر یک (Φ=1 ) و شکل مقطع، محاسبه میشوند.
٢١-٥-١-٥- جرم سازه یکدرجه آزادی معادل
جرم سازه یک درجه آزادی معادل، شامل جرم اعضای سازه ای و جرم تجهیزاتی است که به صـورت دائم روی آن قرار دارند و با تقسیم وزن آنها به شتاب جاذبه بدست میآید.
٢١-٥-١-٦- سختی سازه یکدرجه آزادی معادل
ضریب تبدیل سختی سازه یکدرجه آزادی معادل، با توجه بـه شـرایط تکیـه گـاهی و بـار وارده، از جدول های ٢١-٥-١ تا ٣ محاسبه میشود.
٢١-٥-١-٧- تحلیل سازه یکدرجه آزادی معادل
پس از تعیین مشخصات سازة یکدرجه آزادی معادل، آن را تحت بار دینـامیکی وارده، بـه یکـی از روشهای دینامیکی تحلیل نموده و تغییرشکل حداکثر (ym) محاسبه مـی شـود. بـا انجـام تحلیـل استاتیکی نیز تغییرمکان (ye) تعیین شده و از رابطه ٢١-٥-٣، ضریب شکل پذیری (μ) بـه دسـت میآید. دورانهای تکیهگاهی و وسط دهانه نیز از شکل ٢١-٥-٥ قابل محاسبه است.
تغییرشکل عضو،صرفاً بر اثر بارهای ناشی از انفجار محاسبه شده و فرض مـی شـود بارهـای عـادی طراحی بر تغییرشکل عضو بی تاثیر است. فـرض بـرآن اسـت کـه انـرژی کرنشـی معـادل، گشـتاور خمشی، نیروی برشی، تغییرمکان، سرعت و شتاب سازه یک درجه آزادی، برابر پاسخ نقاط کنترلـی سازه اصلی باشد. نقاط کنترل،معمولاً نقاطی از سازه هستند که بیشترین پاسـخ سـازه ای را دارنـد (مانند محل مفصل خمیری داخل دهانه و یا تکیهگاه گیردار عضو).
٢١-٥-٢- ترکیبات بارگذاری
بارهای انفجار، تنها با بارهایی که به هنگام آن حضور دارند، ترکیب می شوند. بنابراین، بار انفجار بـا بار زلزله و باد ترکیب نمیشود. ترکیب بارگذاریعموماً مطابق زیر میباشد:
| (6-5-21) |
1/2(DL)+0/5(LL)+1/0(BL) یا 0/9 |
٢١-٥-٣- معیارهای پذیرش رفتار عضو سازه ای
معیارهای پذیرش طراحی اعضای سازه ای در مقابل انفجار، شامل محدودیت هایی است که در موارد زیر اعمال میشود:
الف- سطوح عملکرد سازه ای
ب- محدودیت تغییر شکل اعضاء (شامل ضریب شکلپذیری μ و میزان دوران حداکثر θm)
پ- محدودیت تغییرشکل جانبی نسبی طبقات
معمولاً ملاحظات بهره برداری مربوط به طراحی متعارف سازه ها، در سازه های مقاوم در برابر انفجـار موردنظر قرار نمیگیرند.
الف- سطوح عملکرد
سطوح عملکرد مطابق جدول ٢١-١-٤ فصل اول این مبحث تعیین میشوند.
ب- محدودیت تغییر شکل اعضاء (ضوابط پذیرش)
محدودیت های تغییر شکل، برای کسب اطمینان از پاسخ مناسب در برابر بارهای انفجـاری، اعمـال می گردند و براساس مفاهیم ایمنی و ضوابط حفاظت در برابر اثرات انفجار، براساس سـطح عملکـرد ساختمان تعیین میشوند.
در طراحی انفجاری میزان تغییر شکل های فراارتجاعی، مبنایی برای قضاوت پذیرش سازه بر اسـاس سطح عملکرد آن می باشد. این محدودیت ها، بر اساس مقادیر آزمایشگاهی یا شواهد تجربی، تعیـین می شوند. از آنجا که بارهای ناشی از انفجار قابل پیش بینی دقیق نیستند، مقـدار محافظـه کارانـه ای برای اطمینان از عملکرد سازه، در نظر گرفته میشود.
روش اولیه برای اندازه گیری پاسخ سازه، تعیـین ضـریب شـکل پـذیری (μ) بـرای اعضـای سـازهای میباشد (رابطه ٢١-٥-٣). این مقدار، مشخصهای از درجه پاسخ غیر ارتجاعی عضو میباشد.
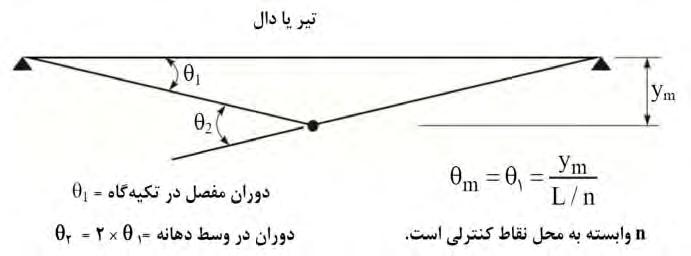
میزان دوران در محل مفصل (θ)، نیز معیار دیگری است که پاسخ تغییر شکل حـداکثر را تـابعی از طول دهانه عضو می نماید و نشان دهنده درصد ناپایداری در نواحی بحرانی عضو میباشد. این مقدار، با دو روش تعیین میشود(شکل ٢١-٥-٥). روش اول تعیین دوران مفصل در تکیهگـاه (θ1) و روش دوم، دوران مفصل در وسط دهانه (θ2) است. در این مبحـث، از روش اول اسـتفاده شـده و مقـادیر مجاز آن، بر اساس سطح عملکرد، در جداول ٢١-٥-٤ تا ٧ ارائه شده است.
اگر عضو سازه ای قاب باشد، باید علاوه بر موارد اخیر ضوابط اضافی دیگـری را نیـز بـرآورده نمایـد.
محدودیت های حرکت جانبی نسبی طبقه (دریفت) به سامانه های قابی شکل جهـت کـاهش خطـر انهدام پیشرونده و کاهش اثرات P-Δ در ستونها، مطابق جدول ٢١-٥-٨ اعمال میگردد.
مقادیر ضریب شکلپذیری (μ) و دوران تکیهگاهی محاسبه شده، باید با مقادیر جداول ٢١-٥-٤ تا ٧ مقایسه شوند تا با توجه به سطح عملکرد مورد نظر، در دامنه مجاز قرار گیرند. این مقادیر، با نوع مصالح و شکل مقطع تغییر می کنند. ضریب شکل پذیری، به عنوان مقیاس اولیه پاسخ برای اعضـا و چرخش مفصل، به عنوان ضابطه کنترل کننده در نظر گرفته میشود.
مقدار ωp به صورت زیر تعریف میشود.
| (7-5-21) |
پ- محدودیت تغییر شکل جانبی قابها
محدودیت تغییر شکل جانبی طبقات مطابق جدول ٢١-٥-٨ میباشد.
| سطح عملکرد | محدودیت تغییر مکان جانبی نسبی طبقات |
| استفاده بی وقفه | |
| ایمنی جانی | |
| استانه فروریزش |
٢١-٥-٤- روش استاتیکی معادل
به عنوان جایگزینی برای روش دینامیکی غیرارتجاعی، می توان از روش اسـتاتیکی معـادل اسـتفاده نمود. این روش میتواند مطابق گام های زیر انجام شود.
گام ١- بارگذاری
برحسب اهمیت سازه، از جدول ٢١-١-٣ فصل ١ فشار طراحی و زمان تداوم آن استخراج میشود.
گام ٢- تبدیل فشار دینامیکی ضربهای به استاتیکی معادل
با محاسبه ضریب بار دینامیکی و ضرب آن در فشار دینـامیکی، فشـار اسـتاتیکی معـادل محاسـبه میگردد.
برای محاسبه ضریب بار دینامیکی ابتدا باید زمان تناوب اصلی عضـو سـازه ای مـورد نظـر محاسـبه شود. برای تیرها، زمان تناوب اصلی برابر است با:
| (8-5-21) |
که در آن:
C =وزن واحد طول عضو
L =طول عضو
Ed = مدول الاستسیته دینامیکی
I = ممان اینرسی مقطع
g = شتاب ثقل
α = مساوی ٢ برای تیرهای دو سر ساده، مساوی 0/89 برای تیرهای دو سـر گیـردار و 1/28 بـرای تیر یکسر ساده و یکسر گیردار است.
زمان تناوب اصلی دال ها وابسته به مشخصات هندسی، مصالح و شرایط تکیه گاهی آن ها است. برای دالهای مستطیلی زمان تناوب برابر است با:
| (9-5-21) |
که در روابط فوق:
a= ضلع بزرگ دال = جرم واحد سطح دال
D = صلبیت خمشی دال برابر با ، به منظـور تـامین اثـرات تـرك خـوردگی، مقـدار حاصل از رابطهی فوق باید نصف شود.
h = ضخامت دال
𝜐= ضریب
Ed = مدول الاستیسیته دینامیکی بتن
ϕ= ضریبی که با توجه به ابعاد و شرایط تکیه گاهی دال از جدول ٢١-٥-٩ محاسبه میشود.
| ضریب ϕ | شرایط تکیه گاهی |
| ϕ=1/57(1+γ2) |  |
 |
|
 |
|
 |
|
 |
|
 |
علامت هاشور نشان دهنده تکیهگاه گیردار و خط ساده نشان دهنده تکیهگاه مفصلی میباشد.
a= ضلع بزرگ دال
b= ضلع کوچک دال
برای تمامی اعضا می توان با مدل سازی عضو به صورت منفرد؛ زمان تناوب را با استفاده از روش های اجزای محدود و با فرض رفتار ارتجاعی مصالح محاسبه نمود. باید توجه نمود شرایط مرزی عضو تـا حد امکان نمایانگر شرایط مرزی واقعی باشد.
سپس با استفاده از شکل ٢١-٥-٦ ضریب بار دینامیکی محاسبه می شـود. در ایـن شـکل td مـدت زمان تأثیر نیروی دینامیکی و T زمان تناوب اصلی عضو میباشد.

فشار استاتیکی معادل وارد بر عضو از رابطهی ٢١-٥-١٠ محاسبه میگردد:
| (10-5-21) |
Wu = فشار استاتیکی معادل وارد بر عضو
d = ضریب بار دینامیکی
W = فشار ناشی از انفجار مطابق گام ١
گام ٣- طراحی
برای هر عضو حداکثر فشار قابل تحمل باید برمبنای مقاومت نهایی آن هـا محاسـبه شـود. ظرفیـت خمشی نهایی تیرها و دال ها براساس تحلیل خمیری و نظریـه خطـوط گسـیختگی از جـدول هـای ٢١-٥-١١ تا ٢١-٥-١٣ محاسبه می گردد. در محاسبه ی ظرفیت خمشی اعضا، ضرایب ایمنیدر ϕ ضریب ١/١ ضرب می شوند (ϕd=1/1ϕ). ضرایب اضافه مقاومت مصالح شامل ضـرایب SIF و DIF نیز با مقادیر مناسب در محاسبات لحاظ می شـود. بـا اسـتفاده از جـداول ٢١-٥-١١ تـا ٢١-٥-١٣ برمبنای ظرفیت خمشی، حداکثر بار گسترده ی (Wr ) محاسبه میگردد.
ضریب اطمینان عضو (نسبت Wr به Wu ) نباید از ضرایب اطمینـان منـدرج در جـدول ٢١-٥-١٠ کمتر شود. ضریب اطمینان سازه براساس سطح عملکرد مفروض برای آن تعیین میگردد.
| سطح عملکرد | ضریب اطمینان |
| استفاده بی وقفه | 1/75 |
| ایمنی جانی | 1/0 |
| آستانه فروریزش | 0/8 |
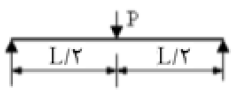
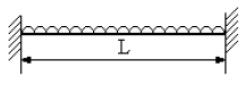
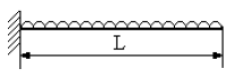
| مقاومت نهایی | شرایط تکیه گاهی و بارگذاری |
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
MP = لنگر خمیری مثبت
MN = لنگر خمیری منفی
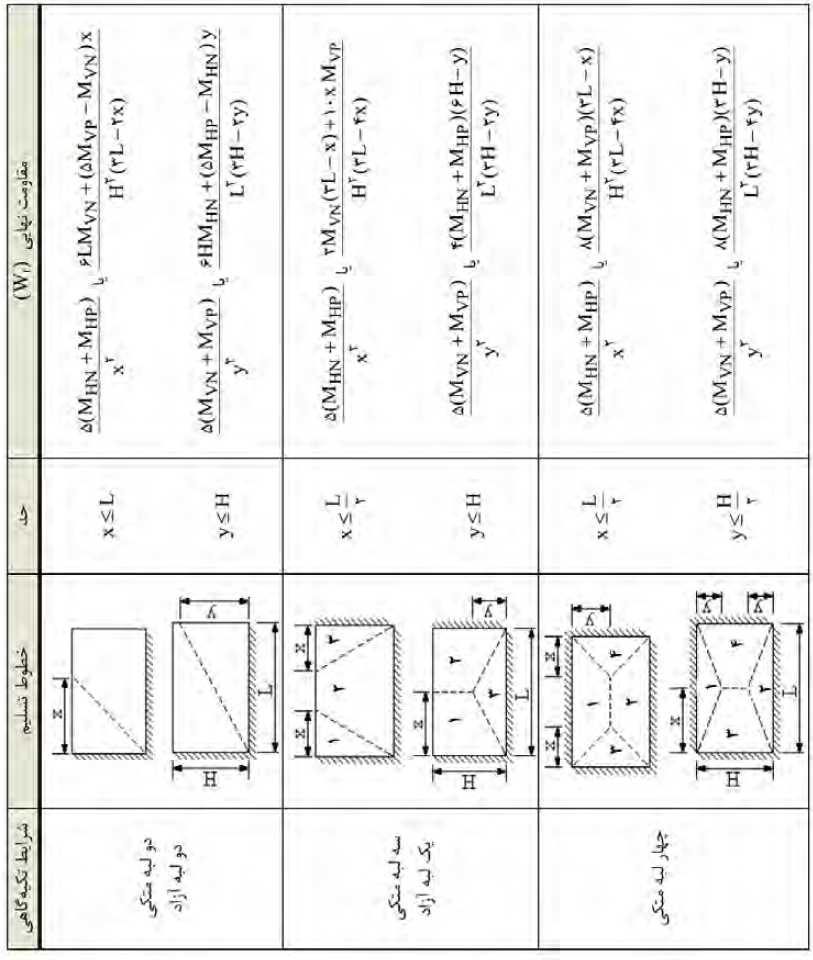
جدول ٢١-٥-١٢- ظرفیت نهایی دالهای دوطرفه (خطوط تسلیم متقارن)
MHP= لنگر خمیری مثبت در راستای ضلع H
MHN= لنگر خمیری منفی در راستای ضلع
HMVP = لنگر خمیری مثبت در راستای ضلع V
MVN = لنگر خمیری منفی در راستای ضلع V
جدول ٢١-٥-١٣- ظرفیت نهایی دالهای دوطرفه (خطوط تسلیم غیرمتقارن)
[1] – از این به بعد این عبارت به صورت ساده ارتجاعی- خمیری بیان می شود.